РАДИОЭЛЕКТРОНИКА И ЭЛЕКТРОТЕХНИКА

В двигателе последовательного возбуждения, который иногда называют сериесным, обмотка возбуждения включена последовательно с обмоткой якоря (рис. 1). Для такого двигателя справедливо равенство I_в=I_a=I, следовательно, его магнитный поток Ф зависит от нагрузки Ф=f (I_a). В этом главная особенность двигателя последовательного возбуждения и она определяет его свойства.

Рис. 1  — Схема электродвигателя последовательного возбуждения

Скоростная характеристика представляет зависимость n=f (I_a) при U=U_н. Она не может быть точно выражена аналитически во всем диапазоне изменения нагрузки от холостого хода до номинальной из-за отсутствия прямой пропорциональной зависимости между I_a и Ф. Приняв допущение Ф=кI_a, запишем аналитическую зависимость скоростной характеристики в виде

При увеличении тока нагрузки гиперболический характер скоростной характеристики нарушается и приближается к линейному, так как при насыщении магнитной цепи машины с увеличением тока I_a магнитный поток остается практически постоянным (рис. 2). Крутизна характеристики зависит от величины Σr.

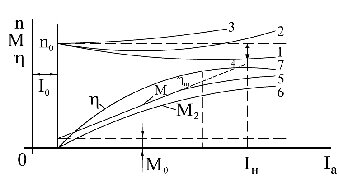
Рис. 2 — Скоростные характеристики двигателя  последовательного возбуждения

Таким образом, скорость сериесного двигателя резко изменяется с изменением нагрузки и такая характеристика называется «мягкой».

При малых нагрузках (до 0,25 I_н) скорость двигателя после­довательного возбуждения может возрасти до опасных пределов (двигатель идет «вразнос»), поэтому работа таких двигателей на холостом ходу не допускается.

Моментная характеристика — это зависимость M=f (I_a) при U=U_н. Если предположить, что магнитная цепь не насыщена, то Ф=кI_a и, следовательно , имеем

М=с_мI_aФ=с_мкI_a²

Это уравнение квадратичной параболы.

Кривая моментной характе­ристики изображена на рисунке 3.8. По мере увеличения тока I_a  магнитная система двигателя насыщается, и характеристика постепенно приближается к прямой.

Рис. 3 — Моментная  характеристика двигателя  последовательного возбуждения

Таким образом, электродвигатель последовательного возбуждения развивает момент, пропорциональный I_a², что и определяет главное его преимущество. Так как при пуске I_a=(1,5...2) I_н, то двигатель последовательного возбуждения развивает значительно больший пусковой момент по сравнению с двигателями параллельного возбуждения, поэтому он широко используется в условиях тяжелых пусков и при возможных перегрузках.

Механическая характеристика представляет собой зависимость n=f (M) при U=U_н. Аналитическое выражение этой характеристики может быть получено только в частном случае, когда магнитная цепь машины ненасыщенна и поток Ф пропорционален току якоря I_a. Тогда можно записать

Решая совместно уравнения , получаем

т.е. механическая характеристика двигателя последовательного возбуждения, также как и скоростная, имеет гиперболический характер (рис. 4).

Рис. 4 — Механические характеристики двигателя последовательного возбуждения

Характеристика КПД двигателя последовательного возбуждения имеет обычный для электродвигателей вид (рис. 2 ).

Электродвигателем параллельного возбуждения называется двигатель постоянного тока, обмотка возбуждения которого включена параллельно обмотке якоря (рис. 1). При снятии характеристик к цепи якоря подводится номинальное напряжение U_н=const.

Рис. 1 — Схема двигателя параллельного возбуждения

Ток, потребляемый двигателем из сети, определяется суммой I=I_a+I_в, ток возбуждения обычно равен I_в=(0,03...0,04) I_н. Все характеристики двигателя снимаются при постоянных сопротивлениях в цепях возбуждения r_в=const и якоря

Σr = const.

 

Скоростная характеристика.

Зависимость n=f (I_a) при U_н=const и I_в=const

Из уравнения ЭДС для электродвигателя

 

имеем

Как видно из выражения,частота вращения двигателя зависит от двух факторов — изменения тока нагрузки и потока. При увеличении тока нагрузки падение напряжения в сопротивлении цепи якоря увеличивается, а частота вращения двигателя уменьшается.

Поперечная реакция якоря размагничивает двигатель, т.е. с ростом тока I_a уменьшается поток и, следовательно, увеличиваются обороты двигателя. Таким образом, оба фактора действуют в отношении оборотов машины встречно и вид скоростной характеристики будет определяется их результирующим действием.

На рис. 2  показаны три разные скоростные характеристики двигателя (кривые 1,2,3). Кривая 1 — скоростная характеристика при преобладании влияния I_a∑r,кривая 2 — оба фактора приблизительно уравновешиваются, кривая 3 — преобладает фактор размагничивающего действия реакции якоря.

Рис. 2 — Характеристики двигателя параллельного возбуждения

Ввиду того, что в реальных двигателях изменение потока Ф незначительно, скоростная характеристика является практически прямой линией. На ряде современных машин параллельного возбуждения для компенсации влияния поперечной реакции якоря устанавливается дополнительная стабилизирующая обмотка возбуждения, которая полностью или частично компенсирует влияние реакции якоря.

Нормальной формой скоростной характеристики, при которой обеспечивается устойчивая работа двигателя, является характеристика вида кривой 1.

Наклон характеристики определяется величиной сопротивления цепи якоря Σr без учета реакции якоря. Когда добавочных сопротивлений в цепь якоря не включено, характеристика называется естественной. Естественная характеристика двигателя параллельного возбуждения достаточно жесткая. Обычно , где n_o — частота вращения при холостом ходе. При включении в цепь якоря добавочных сопротивлений R_рг, наклон характеристик увеличивается, они становятся «мягкими» и называются искусственными или реостатными.

Моментная характеристика – это зависимость М=f (I_a) при r_в=const, U=U_н и Σr=const. В установившемся режиме работы двигателя согласно

имеем M_эм = M₂+M₀ = с_мI_aФ. Если бы в процессе работы машины поток Ф не изменялся, то моментная характеристика представляла бы собой прямую (характеристика 4, рисунок 2). В действительности поток Ф с ростом тока I_a несколько уменьшается из-за размагничивающего действия реакции якоря, поэтому моментная характеристика слегка наклонена вниз (кривая 5). Характеристика полезного момента располагается ниже кривой электромагнитного момента на величину момента холостого хода (кривая 6).

Характеристика КПД η=f (I_a) снимается при U=U_н, r_в=const, Σr=const и имеет типичный для электродвигателей вид (характеристика 7 на рис. 2). КПД быстро растет при увеличении нагрузки от холостого хода до 0,25Р_н , достигает максимального значения при Р=(0,5...0,75) Р_н, а затем до Р=Р_н остается почти неизменным. Обычно в двигателях малой мощности η=0,75...0,85, а в двигателях средней и большой мощности η=0,85...0,94.

Механическая характеристика представляет зависимость n=f (M) при U=U_н, I_в=const и Σr=const. Аналитическое выражение для механической характеристики можно получить из уравнения ЭДС электродвигателя

Определив ток I_а из выражения М = с_еI_aФ и подставив это значение тока в выражение выше, получим

Если пренебречь реакцией якоря и считать, что поток Ф не изменяется, то механические характеристики электродвигателя параллельного возбуждения можно представить в виде прямых (рис. 3), наклон которых зависит от величины сопротивления R_рг включенного в цепь якоря. При R_рг=0 характеристика называется естественной.

Рис. 3 — Механические характеристики двигателя параллельного возбуждения

Следует помнить, что при обрыве цепи возбуждения I_в=0 обороты двигателя n→∞, т.е. двигатель идет «вразнос», поэтому его необходимо немедленно отключить от сети.

Принцип обратимости электрических машин. Двигатели постоянного тока по конструкции не отличаются от генераторов и, как отмечалось, электрические машины постоянного тока могут работать как в режиме генератора, так и в режиме двигателя, т.е. являются обратимыми. Допустим, что машина работает в режиме генератора на сеть с постоянным напряжением U=const и развивает тормозной (по отношению к первичному двигателю) момент M_т (рис.1).

Для  этого режима справедливы соотношения

где ∑r- полное сопротивление цепи якоря.

Рис. 1 — Генераторный и двигательный режимы  машины постоянного тока

Если уменьшать ЭДС Е_агенератора, уменьшая его частоту вращения или магнитный поток Ф, то будет уменьшаться и ток I_a. Когда Е_а станет меньше напряжения U, ток I_a изменит свое направление, однако, посколь­ку U=const, направление тока I_a в обмотке возбуждения, а следовательно и полярность основных полюсов останутся без изменения. При этих условиях изменяется знак электромагнитного момента М_г и машина переходит в двигательный режим, т.е. если прежде она работала генератором, преобразовывая механическую мощность в электрическую, то теперь она потребляет электрическую мощность, преобразовывая эту мощность в механическую и развивая на валу вращающий момент М_д. При этом машина продолжает вращаться в прежнем направлении. Если отсоединить первичный двигатель и приложить к валу машины момент сопротивления механизма М_с, то он будет преодолеваться электромагнитным моментом М_эм.

Классификация двигателей постоянного тока.

Аналогично генераторам, двигатели постоянного тока классифицируются по способу включения обмотки возбуждения по отношению к обмотке якоря — независимого, параллельного, последовательного и смешанного возбуждения. Схемы двигателей и генераторов с перечисленными способами возбуждения одинаковы и приведены на (рис. 1.). Все типы двигателей в зависимости от вида возбуждения имеют различные характеристики, но в основе их работы лежит один и тот же энергетический процесс, характеризуемый уравнениями равновесия ЭДС и моментов.

Уравнение ЭДС двигателя в установившемся режиме работы имеет вид

ЭДС Е_а в обмотке якоря направлена встречно приложенному напряжению, поэтому ее называют противо ЭДС.

Энергетическая диаграмма.

Энергетический процесс рассмотрим на примере двигателя параллельного возбуждения с помощью энергетической диаграммы (рис.2). Двигатель потребляет из сети мощность P₁=U (I_a+I_в). Часть этой мощности тратится на покрытие потерь на возбуждение ΔP_в=UI_в и потери в цепи якоря ΔР_э=I_a²Σr.

Рис. 2 — Энергетическая диаграмма

Оставшаяся часть мощности представляет собой электромагнитную мощность якоря P_эм, которая преобразовывается в полную механическую мощность

P_эм= U (I_a+I_в) - UI_в — I_a²

Полезная механическая мощность P₂, отдаваемая двигателем рабочему механизму, меньше мощности P_эм на величину потерь холостого хода ΔP_о, включающих потери в стали якоря ΔP_ст и механические потери P_мех (трение в подшипниках, вентиляционные и т.д.)

 P₂= P_эм— ΔP_o = P_эм — (ΔP_c — ΔP_мех)

Полезная мощность P₂ обозначается на заводском щитке машины.

Аналогично происходит энергетический процесс в двигателях других типов.

Уравнение равновесия моментов.

Уравнение вращающих моментов в установившемся режиме можно получить, разделив все члены равенства на W (угловую скорость вращения двигателя)

где М₂ — момент сопротивления рабочего механизма; М_о-момент холостого хода.

Вращающий электромагнитный момент равен

Таким образом, вращающий электромагнитный момент расходуется на уравновешивание двух тормозящих моментов:

— момента сопротивления рабочего механизма М₂  ;

— момента холостого хода М_о, соответствующего потерям Р_о=Р_с+Р_мх.

Момент М₂ называется полезным моментом, т.к. он соответствует полезной мощности двигателя Р₂. В неустановившемся режиме скорость двигателя изменяется и на его валу возникает динамический момент. Уравнение равновесия мо­ментов в таких режимах приобретает вид

где М_ст =М₂ +М_о -статический момент сопротивления;

 — динамический момент.

В зависимости от того, уменьшается или увеличивается частота вращения двигателя, динамический момент может быть отрицательным или положительным, т.е. в переходных режимах на валу двигателя создается момент М_j, который препятствует изменению скорости вращения двигателя и механизма. В установившемся режиме динамический момент М_j=0.

Характеристики двигателей постоянного тока.

Рабочие свойства электродвигателей постоянного тока оцениваются следующими характеристиками:

1. Пусковые характеристики, которые оценивают пусковые свойства электродвигателя. К ним относятся:

— кратность пускового тока; где I_ап - пусковой ток ;  I_ан— номинальный ток нагрузки;

 

— кратность пускового момента; где М_п=с_мI_апФ_п;

 

— t_п -время пуска;

— экономичность пуска (стоимость пусковой аппаратуры, пусковые потери).

2. Рабочие характеристики, под которыми понимают зависимости n, M и h от полезной мощности P₂ или тока якоря I_a при постоянных значениях напряжения U_с, сопротивления цепи якоря ∑rи сопротивления цепи возбуждения r_в. Зависимость n=f (P₂) называют скоростной характеристикой, зависимость М=f (P₂) — моментной характеристикой.

3. Механическая характеристика, представляющая собой зависимость n=f (M) при постоянных значениях U_н, r_а, r_в.

4. Регулировочные характеристики, к которым относятся:

— диапазон регулирования скорости n_max/n_min;

— экономичность регулирования (потери, стоимость аппаратуры);

— характер регулирования (плавность);

— простота, надежность и компактность регулировочной аппаратуры.

Информация о журнале
Название журнала: Радиоаматор
Год выхода: 2013
Месяц выхода: январь
Номер журнала: №1
Формат журнала: PDF
Количество страниц: 64
Качество журнала: высокое
Язык: русский
Размер файла: ~39 Мегабайт

(далее…)